Alan Malek

About me

I am a visiting scholar at the Simons Institute for the Theory of Computing. Previously, I was a post-doc with Sasha Rakhlin and Ali Jadbabaie at MIT and completed my PhD under Peter Bartlett at UC Berkeley.

Contact

amalek@mit.edu

Thesis

Alan Malek. Efficient Sequential Decision Making, Diss. University of California, Berkeley, 2017. pdf

Publications

Yasin Abbasi-Yadkori, Peter L. Bartlett, Xi Chen, Alan Malek. Large-Scale Markov Decision Problems via the Linear Programming Dual, arXiv:1901.01992 [math.OC], 2019 pdf.

Alan Malek, Peter L. Bartlett. Horizon-Independent Minimax Linear Regression, In Advances in Neural Information Processing Systems 31, December 2018. pdf poster

Yasin Abbasi-Yadkori, Peter L. Bartlett, Victor Gabillon, Alan Malek, Michal Valko. Best of Both Worlds: Stochastic and Adversarial Best-arm Identification, In Proceedings of The 31th Conference on Learning Theory, July 2018. pdf poster

Jason Altschuler, Victor-Emmanual Brunel, Alan Malek. Best Arm Identification for Contaminated Bandits, arXiv:1802.09514 [math.ST], 2018 pdf.

Wojciech Kotłowski, Wouter M. Koolen, Alan Malek. Random Permutation Online Isotonic Regression, In Advances in Neural Information Processing Systems(NIPS) 30, December 2017. pdf poster

Alan Malek, Yinlam Chow, Mohammad Ghavamzadeh, Sumeet Katariya. Sequential Multiple Hypothesis Testing with Type I Error Control, In Proceedings of AISTATS, April 2017. pdf poster

Yasin Abbasi-Yadkori, Alan Malek, Peter Bartlett, Victor Gabillon. Hit-and-Run for Sampling and Planning in Non-Convex Spaces, In Proceedings of AISTATS, April 2017. pdf

Wojciech Kotłowski, Wouter M. Koolen, Alan Malek. Online Isotonic Regression, In Proceedings of The 29th Conference on Learning Theory, June 2016. pdf

Wouter M. Koolen, Alan Malek, Peter L. Bartlett, Yasin Abbasi-Yadkori. Minimax Time Series Prediction. In Advances in Neural Information Processing Systems(NIPS) 28, December 2015. pdf poster

Yasin Abbasi-Yadkori, Peter Bartlett, Xi Chen, Alan Malek. Large-Scale Markov Decision Problems with KL Control Cost and its Application to Crowdsourcing. In International Conference on Machine Learning (ICML), July 2015. pdf poster slides

Peter Bartlett, Wouter Koolen, Alan Malek, Eiji Takimoto and Manfred Warmuth. Minimax Fixed-Design Linear Regression. In Proceedings of The 28th Conference on Learning Theory, July 2015. pdf poster slides

Wouter M. Koolen, Alan Malek, Peter L. Bartlett. Efficient Minimax Strategies for Square Loss Games. In Advances in Neural Information Processing Systems(NIPS) 27, December 2014. pdf poster

Alan Malek, Yasin Abbasi-Yadkori, Peter Bartlett. Linear Programming for Large-Scale Markov Decision Problems. In International Conference on Machine Learning (ICML), July 2014. pdf slides

Talks

Minimax Strategies for Square Loss, Linear Regression, and Time-series Prediction. Machine Learning Seminar, MIT. August 2016. slides

Minimax Strategies for Square Loss Games. Artificial Intelligence and Reinforcement Learning Seminar, University of Alberta. July 2016. slides

Planning in Large-Scale Markov Decision Problems. CMU. June, 2016. slides

Sequential decision making: modeling how we interact with the world. Keynote, Research Symposium. Harker High School. April 2016. slides

Large-Scale Markov Decision Problems with KL Control Cost and its Application to Crowdsourcing. ICML. July 2015. slides

Linear Programming for Large-Scale Markov Decision Problems. ICML. July 2014. slides

Research Interests

My interests lie between optimization, machine learning, and randomized algorithms. Here is a short description of a few areas and projects:

Minimax Analysis in Online Learning

The major strength of most online learning algorithms (e.g. hedge, follow the perturbed leader) is that we can prove very strong guarantees on their performance. Typically, we have regret bounds that hold for any (potentially adversarial) sequence of inputs and often we have lower bounds that show that any algorithm can be made to suffer regret of the same order. However, in certain cases, we are able to tractably compute the exact minimax algorithm of certain online learning games. Here, I mean minimax in the game-theoretical sense (and not the statistics sense, which again is a statement about matching orders). Finding the minimax algorithm comes with the strongest regret guarantee: for any other algorithm, there is a data sequence that causes at least as much regret that the minimax algorithm would suffer. Specific problems I'm interested in:

We have the minimax algorithm for fixed-horizon squared loss. What other online settings can we compute? E.g. linear regression, online PCA, regression with Bregman loss?
The number of loss function/value function pairs with tractable minimax algorithms is very small. How far can we go in enumerating them?
Even the most famous minimax algorithm, Normalized Maximum Likelihood, is frequently uncomputable (i.e. exponential complexity in the game length). When can we efficiently compute it?

Sequential Hypothesis Testing

In classical, Neyman-Pearson statistical hypothesis testing, a fixed sample size 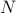and decision region is calculated at the start of the test and no statistically correct conclusions can be made before the sample size is reached. This is because only the statistical deviation at is accounted for; there is no control over the rest of the statistic's sample path. Now if we get data that is much easier than expected, there is no way to adjust the sample size without loosing control on type I and type II errors. However, such statistics and decision boundaries do exist and have been known since at least Wald's SPRT (sequential probability ratio test).

What other sequential tests exist with type I and II error control?
How can we extend these techniques to multiple hypothesis testing?
In ML, the Multi-Arm Bandit problem (especially the best-arm variant) is well studied. What is the intersection? Can the dynamic allocation strategies be easily lifted to multiple hypothesis testing?

Very Large-state space Markov Decision Processes

The planning problem for MDPs assumes full knowledge of the MDP dynamics and loss function and asks: what is the optimal policy? Traditional approaches, such as Value Iteration, scale quadratically in the number of states which becomes prohibitively expensive. If we restrict to some low dimensional family of policies, how well can we do? What conditions do we need to obtain algorithms that scale with the dimension of this family but not with the original state-space?

Efficient policy optimization algorithms that can complete with the best policy in a low-dimensional parametric class.
Extending previous results to have stronger guarantees on special problems, e.g. MDPs with reversible policies

Applications of random Walks to learning and optimization

There is a celebrated thread of papers in Theoretical Computer Science about the volume of a convex body problem. Though exact volume computations are exponential in dimension, over the last two outcomes, increasingly efficient polynomial time algorithms have been developed which all rely on the ability to generate uniform samples with some random walk over convex sets. As a consequence, we can now use random walks to sample efficiently from more general distributions e.g. log-concave distributions, and as a further consequence, optimize some non-convex functions via simulated annealing.

How can we conduct simulated annealing on non-convex spaces?
What implications do the results on sampling from time changing distributions have on online optimization or online algorithms?
How can we Co-opt extensive log-concave mixing time theory (e.g. Langevin dynamics) for regret bounds in online convex optimization?

Teaching

TA for CS 281B/Stat 241B: Statistical Learning Theory II with Prof. Bartlett, Spring 2016
TA for CS 281a/Stat 241a: Statistical Learning Theory I with Prof. Bartlett, Fall 2015
TA for CS 281B/Stat 241B: Statistical Learning Theory II with Prof. Bartlett, Spring 2014
TA for EECS 20N: Signals and Systems with Prof. Abbeel and Prof. Lee, Spring 2011
TA for EECS 20N: Signals and Systems with Prof. Ayazifar and Prof. Anantharam, Fall 2010

Hobbies

I've previous spent a lot of time in a ceramics studio and helped found the Stanford ceramics studio. These days, when I'm not working on my degree, I'm likely to be climbing or cooking, or competing in powerlifting.